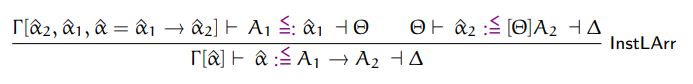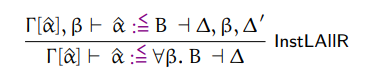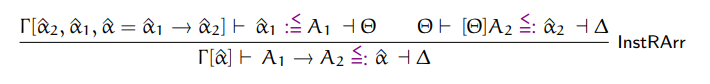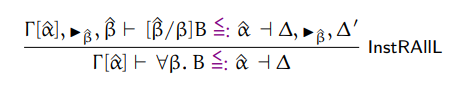Bidirectional type checking step by step

This article is intended for people with little experience in type theory and programming language theory struggling with papers telling them their algorithm is extraordinarily simple before showing this:

After reading Complete and Easy Bidirectional Typechecking for Higher-Rank Polymorphism, I agree that it is actually simple, especially compared to algorithms that require constraint solving and unification. It is simple, but definitely not easy. We have some work ahead of us.

The code is available on this gist if you want to skip ahead and see the full implementation.

Type checking

Type checking is the process that validates expressions against type rules. This is the core of the algorithm we're about to implement.

For the rest of this article, we'll talk about a made up programming language with literals for integers and strings and functions.

The synthesize function

There are two distinct functions at the core of bidirectional type checking that call each other, recursively, in order to resolve the type of an expression. Those functions are synthesize, which infers the type of an expression, and check, which checks if the expression has the expected type. For now it is sufficient to think of their signatures as:

def synthesize(expr)  # returns a type
def check(expr, type) # returns true or false

At this moment, we have no expressions nor types to work with, so let's draw a starting line.

module Expression
  LiteralInt = Data.define(:value)
  LiteralString = Data.define(:value)
end

module Type
  Int = Data.define
  String = Data.define
end

The implementation for synthesize is the following for this set of expressions and types:

def synthesize(expr)
  case expr
  in Expression::LiteralInt
    Type::Int.new
  in Expression::LiteralString
    Type::String.new
  else
    raise "unknown expression"
  end
end

All literal primitives follow this pattern. If we added support for dates, datetimes, regexs, etc., they would all be new entries to this pattern match.

The typing rule for unit (and literals) is described as follows:

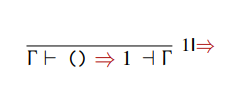
The "1I=>" on the right hand side is the name of the typing rule. "1" means unit, "I" means introduction, and "=>" means synthesis. We can read the name as "the typing rule for synthesizing unit", or "the typing rule for synthesizing literals".

Notice there is a line in the middle with nothing above it. This means that the typing rule has no premises, so it is always true in all contexts. For example, the literal 2 always synthesizes the type Int in all contexts. Contrast this to synthesizing, let's say, a variable named email. Which type should it synthesize? Probably String, but depends, right? The fact that it depends means that the typing rule for variables must have a premise.

We can read the conclusion, what is below the line, as "under context gamma, the unit value synthesizes the type Unit, and produces the same context gamma".

Contexts

For the unit type rule, the context does not matter. Whatever we receive as input we return the same value as output. But this is not the case for other typing rules.

The context is a container that holds symbols, like variable names, function names, module names, etc., and their types (and some other stuff we're about to see). The data structure for context is a list, where the order of the elements in the list is the order they appear in the code. For example, the following code...

let id = 10;
let email = "person@example.org";

...would push id : Int and email : String, in that order, into the context.

Variables

Before we can synthesize the type of a variable we need to add a new constructor to our expression type.

module Expression
  LiteralInt = Data.define(:value)
  LiteralString = Data.define(:value)
+ Variable = Data.define(:name)
end

Then, update the synthesize function with a new pattern.

def synthesize(expr)
  case expr
  in Expression::LiteralInt
    Type::Int.new
  in Expression::LiteralString
    Type::String.new
+ in Expression::Variable(name)
+   # what do we do here?
  else
    raise "unknown expression"
  end
end

To implement the variable case we need to lookup the name in a context. So let's tweak our typing functions to take a context as an argument. The signature I showed earlier was a simplified version. The real signatures of synthesize and check are:

def synthesize(expr, context)  # returns a (type, context)
def check(expr, type, context) # returns context or raises an error if the type is not compatible

The implementation of synthesize, considering the new variable case properly handling context input and output is the following:

def synthesize(expr, context)
  case expr
  in Expression::LiteralInt
    [Type::Int.new, context]

  in Expression::LiteralString
    [Type::String.new, context]

  in Expression::Variable(varname)
    vartype = context.lookup(varname)
    raise "unknown variable" if !vartype
    [vartype, context]

  else
    raise "unknown expression"
  end
end

The literal cases now return the given context as-is. The variable case defers to Context#lookup to retrieve the type of the variable from the context. It then returns the same context without modifications.

We still haven't seen what Context is, and the implementation of Context#lookup, but before we get there, the typing rule for synthesizing variables is the following:

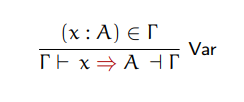
Here's how to read it: "The typing rule for synthesizing variables states that, under context gamma, x synthesizes type A and produces the same context gamma if gamma contains the annotation x : A".

Back to contexts

Contexts contain declarations of quantifications (forall), term variable typings and existentials, both solved and unsolved. The underlying data structure is a list, where the order of the elements represent the order of the facts we have gathered from the program we are type checking.

Let's define the Context type as a list of Element and implement the lookup function we need.

class Context
  module Element
    TypedVariable = Data.define(:name, :type)
  end

  def initialize
    @elements = []
  end

  def lookup(name)
    typed_var =
      @elements.find do |element|
        case element
        in Element::TypedVariable(varname, _) then varname == name
        else false
        end
      end

    typed_var&.then { it.type }
  end
end

W the code above we can successfully synthesize variables.

Annotations

The next typing rule for our language is annotation. It does not matter if the language defines annotation as a separate construct (like Haskell) or if annotations are written next to the expressions (like Typescript).

The rule synthesizing annotations is as follows:

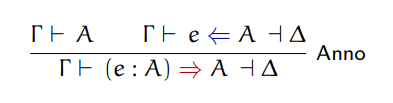
This is a bit more complicated than we have seen so far. The conclusion of this typing rule states that "under context gamma, e has type A synthesizes type A and produces context delta".

Synthesizing type A for the annotation e : A seems kinda redundant, but the premise of the rule provides interesting guarantees. First, A must be well formed. This is denoted by the expression Γ ⊢ A. This ensures that the annotation references a valid type in the program.

The second part of the premise, Γ ⊢ e <= A ⊣ Δ, adds an extra correctness guarantee to the process. The compiler cannot simply trust the annotation and assume e actually have type A. Doing so would make the type system unsound. So instead of trusting, we need to check.

Just to be clear we're on the same page about the notation, e => A is read as "e synthesizes type A" and e <= A is read as "e checks against type A".

This rule is our first encounter with the recursion between synthesizing and checking. In order to synthesizse annotation expression we need to check it, and during checking we might need to synthesize.

Is the type well formed?

The first premise of synthesizing the annotation e : A ensures that the type A is well formed. The following set of rules describe the well-formedness of types:

We can read these rules as:

• UvarWF: A type variable is well formed if it exists in the context. Do not confuse type variables with expression variable.
• UnitWF: The unit type is always well formed. The same is true for all literal types.
• ArrowWF: The function type A -> B is well formed if A and B are well formed.
• ForallWF: The quantification forall x.A is well formed if A is well formed under context gamma with x added to gamma.
• EvarWF: The existential type â is well formed if it exists in the context.
• SolvedEvarWF: The solved existential type â is well formed if it exists in the context.

We haven't talked about type variables, quantification and existentials, but it is useful to see the whole definition. The implementation of this function would look the following for the types we already have:

def type_well_formed?(type, context)
  case type
  in Type::Int then true # UnitWF rule
  in Type::String then true # UnitWF rule
  else raise "unknown type: #{type}"
  end
end

Checking

The second premise of synthesizing the annotation e has type A ensures that the program is not lying to the compiler. It checks that the expression e type checks against A.

In order to implement check we need at least one typing rule, so let's stash the annotation synthesize rule in our head and look at the simplest rule for checking literals:

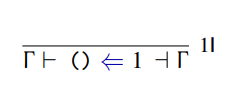
This is very, very similar to the rule for synthesizing literals. The only difference is that arrows are flipped. The implementation of check is as follows:

def check(expr, type, context)
  case [expr, type]

  in [Expression::LiteralInt, Type::Int]
    context

  in [Expression::LiteralString, Type::String]
    context

  else
    raise "type mismatch: #{expr} #{type}"
  end
end

Instead of returning bools to indicate if it typed checked or not, we're going to raise an error when a type mismatch occurs, and we're going to successfully return when valid.

Back to synthesizing annotations

We now have enough structure in place to synthesize annotations.

module Expression
  LiteralInt = Data.define(:value)
  LiteralString = Data.define(:value)
  Variable = Data.define(:name)
+ Annotation = Data.define(:expression, :type)
end

def synthesize(expr, context)
  case expr
  in Expression::LiteralInt
    [Type::Int.new, context]

  in Expression::LiteralString
    [Type::String.new, context]

  in Expression::Variable(varname)
    vartype = context.lookup(varname)
    raise "unknown variable" if !vartype
    [vartype, context]

+ in Expression::Annotation(e, type)
+   raise "invalid type" if !type_well_formed?(type, context)
+   delta = check(e, type, context)
+   [type, delta]

  else
    raise "unknown expression"
  end
end

Checkpoint 01

So far our implementation allows the following expressions to be typed:

synthesize(
  Expression::LiteralInt.new(42),
  Context.new
) # => #<data Type::Int>

synthesize(
  Expression::Annotation.new(
    Expression::LiteralString.new("hello"),
    Type::String.new
  ),
  Context.new
) # => #<data Type::String>

synthesize(
  Expression::Annotation.new(
    Expression::LiteralString.new("hello"),
    Type::Int.new
  ),
  Context.new
) # => type mismatch (RuntimeError)

Lambdas

The typing rule for synthesizing lambdas (anonymous functions) is the following:

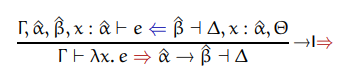
This rule introduces a new concept we haven't talked about yet: existential types. The symbol ^ is used exclusively to denotate existentials. The conclusion of this typing rule is read as: "Under context gamma, lambda from x to e synthesizes the type lambda from existential alpha to existential beta and produces a new context delta".

Existential types can be thought of as unknown types. They're unknown up to this point of the type checking process, but we can gather more information to figure out what they are. Important: they're not like any or void, but placeholder for a type that is yet to be determined.

Alpha and beta are fresh existentials. The word fresh is commonly used in type theory and type checking to refer to newly created variables that are guaranteed to be distinct from other variables currently in scope. To implement this rule, we'll need a function that generates unique names. For simplicity, we'll use a global counter, but feel free to wrap the type checking in a class if you're using an OOP language or a monad that controls state and exceptions if you're using FP language.

$fresh_name_counter = 0
def fresh_name
  $fresh_name_counter += 1
  "x#{$fresh_name_counter}"
end

fresh_name # => "x1"
fresh_name # => "x2"
fresh_name # => "x3"

We can break the the premise of the lambda typing rule into three parts in order to understand it better.

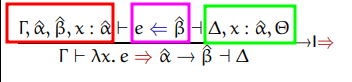
The middle part, highlighted in pink, is a recursive call to check. It checks that e, the body of the function, checks against existential beta.

The first part, highlighted in red, modifies the context gamma by pushing 3 new elements to it: existential alpha, existential beta, and an annotation (typed variable) that x has type existential alpha. This modified context is the context we'll pass to check when checking the body of the function.

The last part, highlighted in green, can be seen as a pattern match. We match on the output of check on x has type existential alpha binding the elements to left to delta and the elements to the right to theta. In other words, take the output of check and split it at the element x : existential alpha. Elements to the left of this split are bound to delta and elements to the right are bound to theta.

Context manipulation

In order to synthesize lambdas we need to manipulate the context with two operations: push, to add new elements to the context, and split to split a context into two at a given element.

class Context
  module Element
    TypedVariable = Data.define(:name, :type)
  end

+ def self.empty = new([])

- def initialize
+ def initialize(elements = [])
-   @elements = []
+   @elements = elements
  end

  def lookup(name)
    typed_var =
      @elements.find do |element|
        case element
        in Element::TypedVariable(varname, _) then varname == name
        else false
        end
      end

    typed_var&.then { it.type }
  end

+ def push(elements)
+   Context.new(@elements + Array(elements))
+ end

+ def split(element)
+   left, right = @elements.partition { it == element }
+   [Context.new(left), Context.new(right)]
+ end
end

Synthesizing lambdas

We need a few extra expressions, types and context elements to synthesize lambdas.

module Expression
  LiteralInt = Data.define(:value)
  LiteralString = Data.define(:value)
  Variable = Data.define(:name)
  Annotation = Data.define(:expression, :type)
+ Lambda = Data.define(:arg_name, :body_expr)
end

module Type
  Int = Data.define
  String = Data.define
+ Variable = Data.define(:name)
+ Existential = Data.define(:name)
+ Lambda = Data.define(:arg_type, :body_type)
end

class Context
  module Element
+   Variable = Data.define(:name)
    TypedVariable = Data.define(:name, :type)
+   UnsolvedExistential = Data.define(:name)
+   SolvedExistential = Data.define(:name, :type)
  end
end

We now have enough to translate the type premises into code with the following implementation.

def synthesize(expr, context)
  case expr
  # ... other expressions

  in Expression::Lambda(arg_name, body_expr)
    alpha_name = fresh_name
    beta_name = fresh_name

    alpha_type = Type::Existential.new(alpha_name)
    beta_type = Type::Existential.new(beta_name)
    lambda_type = Type::Lambda.new(alpha_type, beta_type)

    arg_has_type_alpha = Context::Element::TypedVariable.new(arg_name, alpha_type)

    gamma = context.push([
      Context::Element::UnsolvedExistential.new(alpha_name),
      Context::Element::UnsolvedExistential.new(beta_name),
      arg_has_type_alpha
    ])

    output_context = check(body_expr, beta_type, gamma)
    delta, _theta = output_context.split(arg_has_type_alpha)
    [lambda_type, delta]
  end
end

If we try to synthesize a lambda right now, we'll get a type mismatch error because the check function does not handle existentials yet.

The good news is that, even though it does not work yet, the implementation of synthesize is complete. The bad news is that, due to the recursive nature of the algorithm, we have a deep rabbit hole to get into in order to solve existentials.

Solving existentials

Just to be clear where we're at, when we try to synthesizing a lambda that ignores the argument and returns a constant, we get following error:

puts synthesize(
  Expression::Lambda.new("x", Expression::LiteralInt.new(1)),
  Context.empty
) # =>  # type mismatch: #<data Expression::LiteralInt value=1> #<data Type::Existential name="x2">

This happens when synthesize calls check with the lambda body expression and the beta existential. To fix this problem we need to learn how to check expressions against existentials. The following typing rule helps with that:

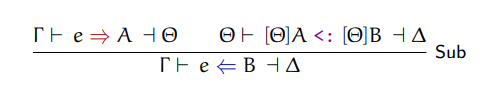
You may read this typing rule as: "Under context gamma, expression e type checks against B and produces context delta if, and only if, under context gamma, expression e synthesizes type A with context output theta and theta applied to A is a subtype of theta applied to B with context output delta.". Sub stands for substitution.

The B type in this rule can be an existential, which we're interested.

But before we can implement this rule, there are two problems we need to solve:

• What does it mean to apply a context to a type?
• What does it mean for a type to be a subtype of another type?

First problem: applying a context to a type

As explained in the paper, "an algorithmic context can be viewed as a substitution for its solved existential variables". Here are the rules:

From top to bottom, we can read each rule as:

• Type variable resolve to itself.
• Unit/literal resolve to itself.
• Existential â solved to type t resolve to context applied to t. Notice the recursion.
• Existential â, unsolved, resolve to itself.
• Lambda A -> B resolve to context applied to A -> context applied to B.
• Quantification ∀a. A resolve to ∀a. context applied to A.

We can implement Contex#apply for the types we already have as following:

class Context
  # ... other methods

  def apply(type)
    case type
    in Type::Int
      type

    in Type::String
      type

    in Type::Variable
      type

    in Type::Existential(name)
      solved_type = find_solved_existential(name)
      solved_type ? apply(solved_type) : type

    in Type::Lambda(arg_type, body_type)
      type.with(arg_type: apply(arg_type), body_type: apply(body_type))

    else
      raise "unknown type: #{type}"
    end
  end

  def find_solved_existential(name)
    solved_existential =
      @elements.find do |element|
        case element
        in Element::SolvedExistential(existential_name, existential_type)
          existential_name == name
        else
          false
        end
      end

    solved_existential&.then { it.type }
  end
end

Second problem: subtyping

If you have a background in OOP languages, it might be natural to associate subtyping with inheritance. This is not the case here. Subtyping is a compatibility relation between two types. When we say A is a subtype of B it means that A can be safely used when B is expected. Think of general substitution instead of inheritance.

Common subtyping relations include function types (covariance and contravariance), record types (a record with name and email is a subtype of a record with name only), union types (int is a subtype of int or string) and refinements (non negative ints is a subtype of int). You can probably think of more examples. When designing a type system for a programming language it is necessary to come up with subtyping rules.

The smallest step we can take into subtyping to unblock our lambda synthesis rule (remember we're still digging the rabbit hole to get back to our lambda synthesis rule), is to implement the following rules:

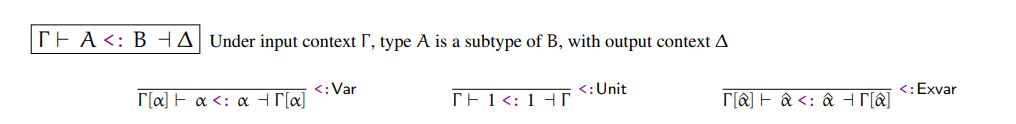
These three rules say the same thing: a type is a subtype of itself. Type variables are a subtype of themselves, literals are a subtype of themselves, and existentials are a subtype of themselves. We can implement this function as follows:

def subtype(type_a, type_b, context)
  case [type_a, type_b]
  in [Type::Int, Type::Int]
    context

  in [Type::String, Type::String]
    context

  in [Type::Variable(name_a), Type::Variable(name_b)]
    raise "subtype mismatch: #{name_a} #{name_b}" if name_a != name_b
    context

  in [Type::Existential(name_a), Type::Existential(name_b)]
    raise "subtype mismatch: #{name_a} #{name_b}" if name_a != name_b
    context

  else
    raise "subtype mismatch: #{type_a} #{type_b}"
  end
end

Back to checking

As a reminder, here is the rule for checking an expression against a type:

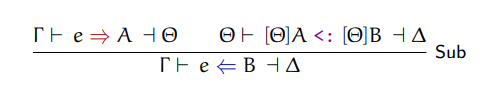
With Context#apply and subtype we now have enough tools to improve our implementation of check:

def check(expr, type, context)
  case [expr, type]

  in [Expression::LiteralInt, Type::Int]
    context

  in [Expression::LiteralString, Type::String]
    context

  else
-   raise "type mismatch: #{expr} #{type}"
+   synthesized_type, theta = synthesize(expr, context)
+   subtype(theta.apply(synthesized_type), theta.apply(type), theta)
  end
end

This change moves our error from "type mismatch" to "subtype mismatch". Progress.

Subtyping against existentials

The rule for subtyping against existentials is the following:

We can read this rule as "under context gamma containing the existential alpha, type A is a subtype of alpha and produces context delta if, and only if, alpha does not occur in A and A can be instantiated to alpha with context output delta."

Instantiation is a new concept we haven't talked about yet, but before we get there, let's talk about the occurs check.

Occurs check

The paper does not provide an implementation for occurs, so we will come up with one ourselves. The problem we're trying to prevent is circular or recursive types that would expand to infinity when instantiated.

def occurs?(name, type)
  case type
  in Type::Int
    false

  in Type::String
    false

  in Type::Variable(var_name)
    var_name == name

  in Type::Existential(existential_name)
    existential_name == name

  in Type::Lambda(arg_type, return_type)
    occurs?(name, arg_type) || occurs?(name, return_type)

  else
    raise "unknown type: #{type}"
  end
end

Back to instantiation

Type instantiation comes in two flavors: left instantiation, where we instantiate an existential against a type, and right instantiation, where we instantiate a type against an existential.

Lambda expression synthesis requires right instantiation because we check the type of the body expression against the beta-existential generated by the synthesis rule.

The smallest step we can take into implementing right instantiation is the following rule:

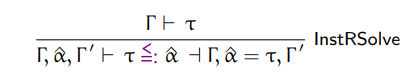
We can read this as: "under context gamma containing alpha, alpha is instantiated to type t if t is well formed and produces context gamma replacing unsolved alpha with alpha solved to t." The notation used for t (lower case tau) suggests that is must be a monotype, so we also need to add this check.

The implementation of monotype? is redundant because we haven't seen quantifications yet, but let's define it anyway so we have a place to extend it later.

def monotype?(type)
  case type
  in Type::Lambda(arg_type, body_type)
    monotype?(arg_type) && monotype?(body_type)

  else
    true
  end
end

def instantiate_right(type, existential_name, context)
  if monotype?(type) && type_well_formed?(type, context)
    return context.replace(
      Context::Element::UnsolvedExistential.new(existential_name),
      Context::Element::SolvedExistential.new(existential_name, type)
    )
  end

  raise "invalid right instantiation: #{type} #{existential_name}"
end

As well as the Context#replace:

class Context
  # ... other methods

  def replace(element_old, element_new)
    elements = @elements.flat_map { |element| element == element_old ? Array(element_new) : element }

    Context.new(elements)
  end
end

We also need to update our type_well_formed? function to support type variables, existentials and lambdas:

class Context
  # ... other methods

  def has?(element)
    @elements.include?(element)
  end
end

def type_well_formed?(type, context)
  case type
  # we only had these two cases before for literal values
  in Type::Int then true
  in Type::String then true

  in Type::Variable(name)
    context.has?(Context::Element::Variable.new(name))

  in Type::Existential(name)
    context.has?(Context::Element::UnsolvedExistential.new(name)) ||
      context.find_solved_existential(name).present?

  in Type::Lambda(arg_type, body_type)
    type_well_formed?(arg_type, context) && type_well_formed?(body_type, context)

  else
    raise "unknown type: #{type}"
  end
end

With these functions in place, we have enough in place to delegate to subtying existentials to right instantiation:

def subtype(type_a, type_b, context)
  case [type_a, type_b]

  in [Type::Int, Type::Int]
    context

  in [Type::String, Type::String]
    context

  in [Type::Variable(name_a), Type::Variable(name_b)]
    raise "subtype mismatch: #{name_a} #{name_b}" if name_a != name_b
    context

  in [Type::Existential(name_a), Type::Existential(name_b)]
-   raise "subtype mismatch: #{name_a} #{name_b}" if name_a != name_b
+   return context if name_a == name_b
+   instantiate_right(type_a, name_b, context)

+ in [_, Type::Existential(existential_name)]
+   raise "circular instantiation: #{type_a} #{type_b}" if occurs?(existential_name, type_a)
+   instantiate_right(type_a, existential_name, context)

  else
    raise "subtype mismatch: #{type_a} #{type_b}"
  end
end

Finally no more errors now when synthesizing this one lambda:

puts synthesize(
  Expression::Lambda.new("x", Expression::LiteralInt.new(1)),
  Context.empty
) # => #<data Type::Lambda arg_type=#<data Type::Existential name="x1">, bodytype=#<data Type::Existential name="x2">>

Although the inferred type looks weird with existentials, it's correct. We're finally out of the rabbit hole, and, good news, we have covered the whole algorithm end to end. There are still gaps in our implementation, but there are no more side tracks or new concepts or new abstractions to learn. Apart from one extra function we have not yet implemented (left instantiation), we'll mostly be modifying our existing functions instead of adding new ones.

Out of the 28 typing rules in the algorithm, we have implemented 11 of them. For visual people, here's the typing rules we've implemented, highlighted in red:

If you want to take a break, it's good time now.

Existentials subtyping existentials

Let's continue our journey by synthesizing the famous identity function λa.a.

If we try to synthesize the identity function we get the following error: "subtype mismatch: x1 x2 (RuntimeError)". This is because our right instantiation function is very limited. The typing rule we need to support now is the following:

This rule states that "under context gamma existential beta is a subtype of existential alpha if, and only if, existential alpha exists in gamma and it is defined in a position before existential beta, with output gamma having existential beta solved to existential alpha".

For practical purposes, we can implement right instantiation to whatever existential appears before the other.

We need to add a helper method on context Context#index that returns the position of an element. Then we can modify instantiate_right to consider subtyping existentials

class Context
  # ... other methods

+ def index(element)
+   @elements.index(element)
+ end
end

def instantiate_right(type, existential_name, context)
  if type_well_formed?(type, context)
    return context.replace(
      Context::Element::UnsolvedExistential.new(existential_name),
      Context::Element::SolvedExistential.new(existential_name, type)
    )
  end

- raise "invalid right instantiation: #{type} #{existential_name}"
+ case type
+ in Type::Existential(beta_name)
+   alpha_name = existential_name
+   alpha = Context::Element::UnsolvedExistential(alpha_name)
+   beta = Context::Element::UnsolvedExistential(beta_name)
+   if context.index(alpha) < context.index(beta)
+     solved = Context::Element::SolvedExistential.new(beta_name, Type::Existential.new(alpha_name))
+     context.replace(beta, solved)
+   else
+     solved = Context::Element::SolvedExistential.new(alpha_name, Type::Existential.new(beta_name))
+     context.replace(alpha, solved)
+   end
+
+ else
+   raise "invalid right instantiation: #{type} #{existential_name}"
+ end
end

We can now synthesize the id function correctly.

puts synthesize(
  Expression::Lambda.new("x", Expression::Variable.new("x")),
  Context.empty
) # => #<data Type::Lambda arg_type=#<data Type::Existential name="x1">, bodytype=#<data Type::Existential name="x2">>

We cannot annotate it yet because we're still missing quantification types.

Quantification types

The signature of the id function is forall a. a -> a. For all is known as universal quantification in the paper. To support quantifications, we need to add the type definition and update our implementation of type_well_formed?, occurs? and Context#apply.

module Type
  # ...
  Quantification = Data.define(:name, :subtype)
end

def type_well_formed?(type, context)
  case type
  # ...
  in Type::Quantification(name, subtype)
    type_well_formed?(subtype, context.push(Context::Element::Variable.new(name)))
  end
end

def monotype?(type)
  case type
  # ...
  in Type::Quantification
    false
  end
end

def occurs?(name, type)
  case type
  # ...
  in Type::Quantification(alpha, subtype)
    name == alpha || occurs?(name, subtype)
  end
end

class Context
  def apply(type)
    case type
    # ...
    in Type::Quantification(name, subtype)
      type.with(subtype: apply(subtype))
    end
  end
end

This gets us closer to annotating the id function, but now we're stuck on subtyping a lambda type with a quantification.

puts synthesize(
  Expression::Annotation.new(
    Expression::Lambda.new("x", Expression::Variable.new("x")),
    Type::Quantification.new("a", Type::Lambda.new(Type::Variable.new("a"), Type::Variable.new("a")))
  ),
  Context.empty
) # subtype mismatch: #<data Type::Lambda arg_type=#<data Type::Existential name="x1">, body_type=#<data Type::Existential name="x2">> #<data Type::Quantification name="a", subtype=#<data Type::Lambda arg_type=#<data Type::Variable name="a">, body_type=#<data Type::Variable name="a">>> (RuntimeError)

The typing rule we need to make progress is the following:

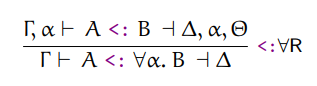
This rule acts like an expansion step to other typing rules. We expand the quantification type by adding the quantification varible to the context, and then call subtype again with this modified context. When returning, we drop the variable. This is what the Delta, alpha, Theta means.

def subtype(type_a, type_b, context)
  case [type_a, type_b]
  # ...
  in [_, Type::Quantification(name, subtype)]
    alpha_var = Context::Element::Variable.new(name)
    gamma = context.push(alpha_var)
    result = subtype(type_a, subtype, gamma)
    delta, _theta = result.split(alpha_var)
    delta
  end
end

With this rule in place we've changed the error from a subtype mistmatch between a lambda and a quantification to a subtype mismatch between two lambdas. The first lambda type is the result from calling synthesize. The second lambda type is the result from expanding the quantification present in the annotation.

subtype mismatch:
#<data Type::Lambda arg_type=#<data Type::Existential name="x1">, body_type=#<data Type::Existential name="x2">>
#<data Type::Lambda arg_type=#<data Type::Variable name="a">, body_type=#<data Type::Variable name="a">>

Subtyping lambdas

The typing rule we need to make progress now is the following:

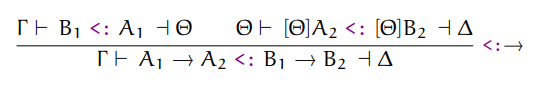
The conclusion is mostly straight forward, but the premise describes an interesting relation for covariance and contravariance. Notice that the subtyping order is different for the argument type and the body type (aka return type). B1 must be a subtype of A1 (argument), while A2 must be a subtype of B2 (return).

We have all the pieces in place to implement this rule, so let's go ahead and modify the subtype function to handle this case.

def subtype(type_a, type_b, context)
  case [type_a, type_b]
  # ...
  in [Type::Lambda(a1, a2), Type::Lambda(b1, b2)]
    theta = subtype(b1, a1, context)
    delta = subtype(theta.apply(a2), theta.apply(b2), theta)
    delta
  end
end

The error changed again. We're now one level deep into the previous error. Progress.

subtype mismatch: #<data Type::Existential name="x2"> #<data Type::Variable name="a">

The existential x2 is the synthesized type for the body of our lambda. The type variable a is the annotation we provided. You might have notice that the existential appears on the left side of the relation instead of the right side. This means we need to look into left instantiation to continue making progress.

Left instantiation

The first typing rule that is going to enable instanting existentials on the left is the following:

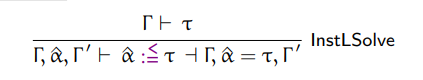
This is very, very similar to the first rule we saw for right instantiation. We can implement it with the following code:

def instantiate_left(type, existential_name, context)
  if monotype?(type) && type_well_formed?(type, context)
    return context.replace(
      Context::Element::UnsolvedExistential.new(existential_name),
      Context::Element::SolvedExistential.new(existential_name, type)
    )
  end

  raise "invalid left instantiation: #{type} #{existential_name}"
end

Then, we can call instantiate_left from subtype as described by the following type rule, which looks very similar to the rule that delegates subtyping to right instantiation:

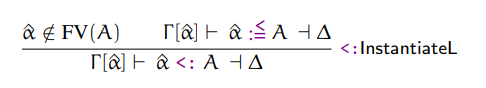
def subtype(type_a, type_b, context)
  case [type_a, type_b]
  # ...
  in [Type::Existential(existential_name), _]
    raise "circular instantiation: #{type_a} #{type_b}" if occurs?(existential_name, type_b)
    instantiate_left(type_b, existential_name, context)
  end
end

We can finally annotate our id function successfully!

puts synthesize(
  Expression::Annotation.new(
    Expression::Lambda.new("x", Expression::Variable.new("x")),
    Type::Quantification.new("a", Type::Lambda.new(Type::Variable.new("a"), Type::Variable.new("a")))
  ),
  Context.empty
) # => #<data Type::Quantification name="a", subtype=#<data Type::Lambda arg_type=#<data Type::Variable name="a">, body_type=#<data Type::Variable name="a">>>

Now that we can define the id function, let's call it with some values to make sure it behaves as expected. So our next is now is calling functions, which is also known as application.

Applications

The rule that describes application synthesis is the following:

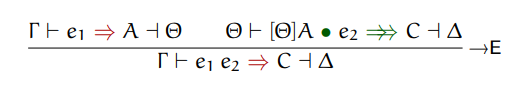
The conclusion states that e2 applied to e1 synthesizes type C. For application to work, e1 must resolve to a lambda and e2 must be a value of the same type as the argument type of the lambda. Just to be clear, e1 does not need to be a literal lambda, it could be a variable that stands for a lambda that we resolve via lookup.

This is our first time seeing the green arrow notation. This notation is similar to regular synthesize but specialized for the result of applying a function to a value.

To apply e1 to e2 we first synthesize e1. This is described in first premise. The result of this synthesis needs to be a lambda, an existential or a quantification. Everything else is invalid. It might be useful to peek ahead some extra typing rules to see the full picture of application synthesizes.

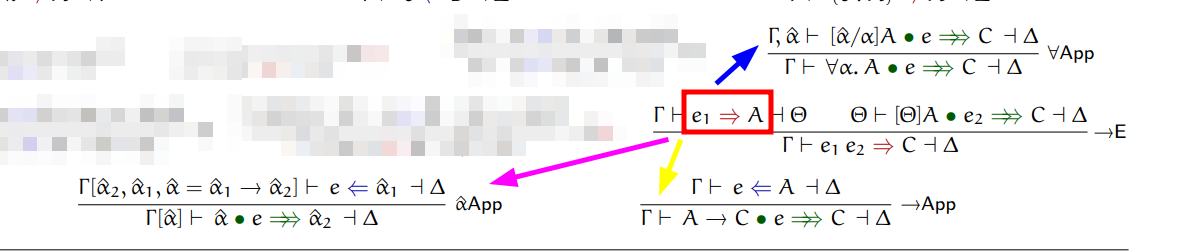
I've highlighted e1 synthesizes A in red. The pink arrow points to the typing rule when A is an existential. The yellow arrow points to the typing rule when A is a lambda. The blue arrow points to the typing rule when A is a quantification, which, as you might have noticed, expands the quantification and calls synthesize again.

The typing rule for quantification describes substitution, which we haven't seen yet. The notation used is [â/a]A. The notation for substitution is famously inconsistent across different papers, but in this case, we can read [â/a]A as "substitute a with â in A".

Substitution

The paper does not provide an implementation for substitution, but we can implement it ourselves.

def substitute(substitution_type, alpha, original_type)
  case original_type
  in Type::Variable(name)
    name == alpha ? substitution_type : original_type

  in Type::Existential(name)
    name == alpha ? substitution_type : original_type

  in Type::Lambda(arg_type, body_type)
    original_type.with(
      arg_type: substitute(substitution_type, alpha, arg_type),
      body_type: substitute(substitution_type, alpha, body_type)
    )

  in Type::Quantification(name, subtype)
    if name == alpha
      original_type.with(subtype: substitution)
    else
      original_type.with(subtype: substitute(substitution_type, alpha, subtype))
    end

  else
    original_type
  end
end

Back to applications

I believe we can implement all four application synthesis rules at once. Let's start with defining an expression for application.

module Expression
  LiteralInt = Data.define(:value)
  LiteralString = Data.define(:value)
  Variable = Data.define(:name)
  Annotation = Data.define(:expression, :type)
  Lambda = Data.define(:arg_name, :body_expr)
+ Application = Data.define(:lambda, :arg)
end

The first step is to handle Expression::Application on the synthesize function and then delegate to synthesize_application to continue into this branch.

def synthesize(expr, context)
  case expr
  # ...
  in Expression::Application(e1, e2)
    a, theta = synthesize(e1, context)
    c, delta = synthesize_application(theta.apply(a), e2, theta)
    [c, delta]
  end
end

Then we can implement synthesize_application with the three typing rules we have seen earlier.

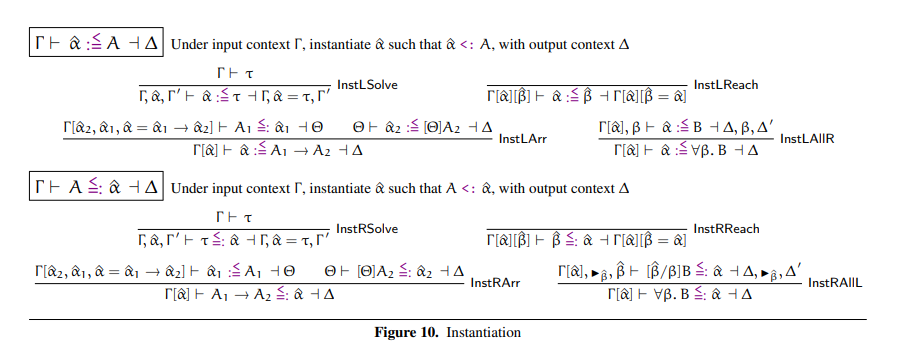
def synthesize_application(lambda_type, arg_expr, context)
  case lambda_type

  # Figure 10. ∀App
  #
  # Γ, â ⊢ [â/a]A·e =>=> C ⊣ Δ
  # --------------------------
  # Γ ⊢ ∀a.A·e =>=> C ⊣ Δ
  in Type::Quantification(alpha, a)
    â_name = fresh_name
    â_unsolved = Context::Element::UnsolvedExistential.new(â_name)
    â_type = Type::Existential.new(â_name)
    gamma = context.push(â_unsolved)
    substituted_a = substitute(â_type, alpha, a)
    synthesize_application(substituted_a, arg_expr, gamma)

  # Figure 10. âApp
  #
  # Γ[â2, â1, â = â1 -> â2] ⊢ e <= â1 ⊣ Δ
  # -------------------------------------
  # Γ[â] ⊢ â·e =>=> â2 ⊣ Δ
  in Type::Existential(â)
    â1_name = fresh_name
    â2_name = fresh_name
    â1 = Context::Element::UnsolvedExistential.new(â1_name)
    â2 = Context::Element::UnsolvedExistential.new(â2_name)
    â_solved = Context::Element::SolvedExistential.new(â, Type::Lambda.new(Type::Existential.new(â1), Type::Existential.new(â2)))
    gamma = context.replace(Context::Element::UnsolvedExistential.new(â), [â2, â1, â_solved])
    delta = check(arg_expr, Type::Existential.new(â1_name), gamma)
    [Type::Existential.new(â2_name), delta]

  # Figure 10. ->App
  #
  # Γ ⊢ e <= A ⊣ Δ
  # -----------------------
  # Γ ⊢ A -> C·e =>=> C ⊣ Δ
  in Type::Lambda(arg_type, body_type)
    delta = check(arg_expr, arg_type, context)
    [body_type, delta]

  else
    raise "unexpected application: #{lambda_type}"
  end
end

With this in place, we can hopefully synthesize an application to our id function and get back the expected type.

id = Expression::Annotation.new(
  Expression::Lambda.new("x", Expression::Variable.new("x")),
  Type::Quantification.new("a", Type::Lambda.new(Type::Variable.new("a"), Type::Variable.new("a")))
)

puts synthesize(
  Expression::Application.new(id, Expression::LiteralInt.new(42)),
  Context.empty
) # => #<data Type::Existential name="x5">

puts synthesize(
  Expression::Application.new(id, Expression::LiteralString.new("foo")),
  Context.empty
) # => #<data Type::Existential name="x8">

Well, that's a little disappointing. But wait! We're still missing one last step to resolve the existential into a meaningful type. We just need to apply the output context to the output type. Let's create a helper function to be the entry point of our algorithm:

def infer(expr)
  type, context = synthesize(expr, Context.empty)
  context.apply(type)
end

With this, we finally have the output we were expecting!

puts infer(
  Expression::Application.new(id, Expression::LiteralInt.new(42))
) # => #<data Type::Int>

puts infer(
  Expression::Application.new(id, Expression::LiteralString.new("foo"))
) # => #<data Type::String>

We have implemented 19 out of the 28 typing rules. We're over 70% of the way there. In fact, we are so close to being done that there is only one more concept we haven't seen.

Context markers

Context markers are placeholders used to facilitate splitting after calling functions that modify the context. We can see the notation in this typing rule:

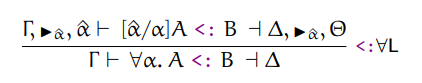
Notice there is a caret symbol pointing right. This is a marker. The only purpose of this marker is being used to split the context after recursively invoking subtype. Notice that delta is everything before the marker, and theta is everything after the marker.

Let's add the marker definition as a context element.

class Context
  module Element
    Variable = Data.define(:name)
    TypedVariable = Data.define(:name, :type)
    UnsolvedExistential = Data.define(:name)
    SolvedExistential = Data.define(:name, :type)
+   Marker = Data.define(:name)
  end
end

This typing rule is a bit tricky. In order to invoke its path, we need to subtype a quantification with another type. The most common way for a quantification to appear on the left of a subtype is when a function accepts another function as an argument. For example:

call42 :: (Int -> Int) -> Int
call42 f = f 42

call42 id

In this example, call42 expects a function Int -> Int, and we provide forall a. a -> a. This is valid, but our type checker currenntly fails with a subtype error telling us that quantification is not a subtype of lambda.

Let's fix this by implementing the typing rule on the subtype function.

def subtype(type_a, type_b, context)
  case [type_a, type_b]
    # ...
    in [Type::Quantification(alpha, a), _]
      â_name = fresh_name
      â_marker = Context::Element::Marker.new(â_name)
      â_unsolved = Context::Element::UnsolvedExistential.new(â_name)
      â_type = Type::Existential.new(â_name)
      substituted_a = substitute(â_type, alpha, a)
      gamma = context.push(â_marker).push(â_unsolved)
      result = subtype(substituted_a, type_b, gamma)
      delta, _theta = result.split(â_marker)
      delta
  end
end

With this we can synthesize our previous example with call42.

id = Expression::Annotation.new(
  Expression::Lambda.new("x", Expression::Variable.new("x")),
  Type::Quantification.new("a", Type::Lambda.new(Type::Variable.new("a"), Type::Variable.new("a")))
)

call42 = Expression::Annotation.new(
  Expression::Lambda.new(
    "f",
    Expression::Application.new(Expression::Variable.new("f"), Expression::LiteralInt.new(42))
  ),
  Type::Lambda.new(
    Type::Lambda.new(Type::Int.new, Type::Int.new),
    Type::Int.new
  )
)

puts infer(Expression::Application.new(call42, id)) # => #<data Type::Int>

The final 8 typing rules...

... will be left as an exercise for the reader 😁. If you're interested in the full implementation, the code is available on this gist.

Here are missing typing rules:

Algorithmic typing

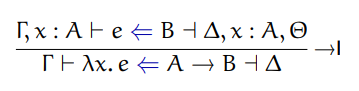
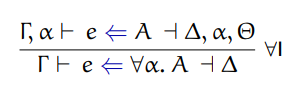
Algorithmic subtyping

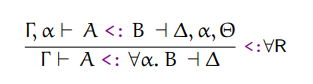
Instantiation